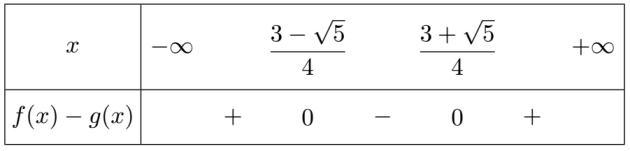Exercices - Signe du trinôme

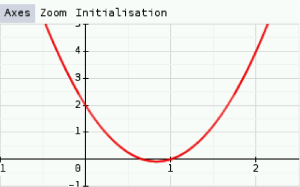
b. \(3x^2-5x+2\) a pour discriminant \(\Delta=(-5)^2-4\times3\times2\color{red}=1>0\).

Le trinôme a donc deux racines réelles :

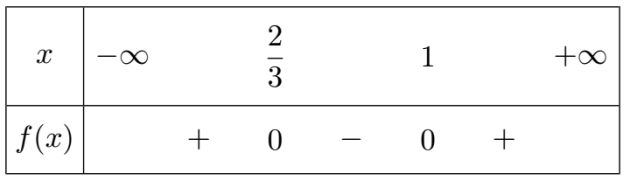
• \(x_1=\frac{5-\sqrt{1}}{2\times3}\color{red}=\frac23\)

• \(x_2=\frac{5+\sqrt{1}}{2\times3}\color{red}=1\)

D'autre part, \(\color{blue}a=3>0\), la parabole est donc tournée vers le haut :

La conjecture émise à la question 1.a. est donc validée.

Le calcul nous a en outre permis de donner la valeur exacte de la racine.

a. \(f(x)-g(x)=3x^2-5x+2-\left(-x^2+x+1\right)\color{blue}=4x^2-6x+1\)

\(4x^2-6x+1\) a pour discriminant \(\Delta=(-6)^2-4\times4\times1\color{blue}=20>0\)

Le trinôme a donc deux racines réelles :

• \(x_1=\frac{6-\sqrt{20}}{2\times4}=\frac{6-2\sqrt{5}}{8}\color{red}=\frac{3-\sqrt{5}}{4}\approx0,19\)

• \(x_2=\frac{6+\sqrt{20}}{2\times4}=\frac{6+2\sqrt{5}}{8}\color{red}=\frac{3+\sqrt{5}}{4}\approx1,31\)

D'autre part \(\color{blue}a=4>0\), la parabole est donc tournée vers le haut :

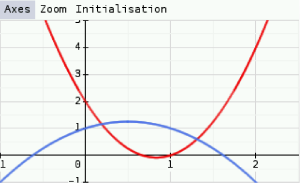
b. On peut en déduire que

• \(\mathscr C_f\) est au-dessus de \(\mathscr C_g\) sur \(\left]-\infty ;\frac{3-\sqrt{5}}{4}\right]\cup\left[\frac{3+\sqrt{5}}{4} ;+\infty\right[\)

• \(\mathscr C_f\) est en-dessous de \(\mathscr C_g\) sur \(\left[\frac{3-\sqrt{5}}{4} ;\frac{3+\sqrt{5}}{4}\right]\)