Exercices - Signe du trinôme

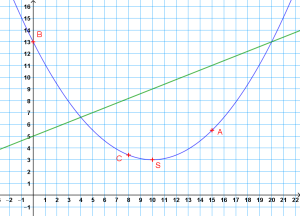
La parabole passe par le point \(B(0 ;13)\) donc \(f(0)=13\).

Or \(f(0)=a\times0^2+b\times0+c=c\).

Donc \(\color{red}\boxed{c=13}\).

La parabole passe par les points \(A(15 ;5,5)\) et \(C(8 ;3,4)\), donc :

\(\begin{array}{rcl}\begin{cases}f(15)=5,5\\f(8)=3,4\end{cases}&\Leftrightarrow&\begin{cases}a\times15^2+b\times15+13=5,5\\a\times8^2+b\times8+13=3,4\end{cases}\\[0.5cm]&\Leftrightarrow&\begin{cases}225a+15b+13=5,5\\64a+8b+13=3,4\end{cases}\\[0.5cm]&\Leftrightarrow&\color{red}\boxed{\begin{cases}225a+15b=-7,5\\64a+8b=-9,6\end{cases}}\end{array}\)

On résout le système par combinaison :

\(\begin{array}{ll}\begin{cases}225a+15b=-7,5\quad\color{magenta}\times8\\64a+8b=-9,6\quad\color{blue}\times(-15)\end{cases}\\[0.5cm]\underline{\begin{cases}{\color{magenta}1800}\,a+{\color{magenta}120}\,b=\color{magenta}-60\\{\color{blue}-960}\,a\,{\color{blue}-120}\,b=\color{blue}144\end{cases}}&\text{on additionne terme à terme}\\\quad840\,a+\quad0\quad=\,84\end{array}\)

Donc \(a=\frac{84}{840}\Leftrightarrow\color{red}\boxed{a=\frac{1}{10}=0,1}\)

On utilise alors la deuxième équation du système :

\(64\times0,1+8b=-9,6\Leftrightarrow6,4+8b=-9,6\Leftrightarrow8b=-16\Leftrightarrow\color{red}\boxed{b=-2}\)

D'après les questions précédentes, \(\color{blue}f(x)=0,1x^2-2x+13\).

Il s'agit d'écrire \(f(x)\) sous sa forme canonique :

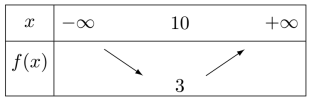
\(\begin{array}{rcl}f(x)&=&0,1x^2-2x+13\\&=&0,1\left(x^2-20x\right)+13\\&=&0,1\left(\left(x-10\right)^2-100\right)+13\\&=&0,1\left(x-10\right)^2-10+13\\&=&\color{red}\underline{0,1\left(x-10\right)^2+3}\end{array}\)

Grâce à la forme canonique, on peut voir que les coordonnées du sommet de la parabole sont \((10 ;3)\).

D'autre part \(a=0,1>0\), la parabole est donc tournée vers le haut.

On étudie le signe de \(f(x)-\left(0,4x+5\right)=0,1x^2-2x+13-0,4x-5=\color{blue}0,1x^2-2,4x+8\)

• \(0,1x^2-2,4x+8\) a pour discriminant \(\Delta=(-2,4)^2-4\times0,1\times8\color{red}=2,56>0\)

  Le trinôme a donc deux racines réelles :

  • \(x_1=\frac{2,4-\sqrt{2,56}}{2\times0,1}=\frac{2,4-1,6}{0,2}=\frac{0,8}{0,2}\color{red}=4\)

  • \(x_2=\frac{2,4+\sqrt{2,56}}{2\times0,1}=\frac{2,4+1,6}{0,2}=\frac{4}{0,2}\color{red}=20\)

• D'autre part \(a=0,1>0\) donc la parabole est tournée vers le haut :

  

Ce qui valide la conjecture faite à la question précédente.