Exercices - Signe du trinôme

\(0,5x^2-0,5x+c\) a pour discriminant \(\Delta=(-0,5)^2-4\times0,5\times c\color{blue}=0,25-2c\)

\(\begin{array}{rcl}\color{blue}\Delta\geqslant0&\Leftrightarrow&0,25-2c\geqslant0\\&\Leftrightarrow&0,25\geqslant2c\\&\Leftrightarrow&\color{blue}0,125\geqslant c\end{array}\)

On en déduit que l'équation \(P(x)=0\) a :

• 2 solutions réelles lorsque \(\color{red}c<0,125=\frac18\)

• 1 solution réelle lorsque \(\color{red}c=0,125\)

• aucune solution lorsque \(\color{red}c>0,125\)

• \(0,5x^2-0,5x-1\) a pour discriminant \(\Delta=(-0,5)^2-4\times0,5\times(-1)=2,25\color{red}\color{red}=\frac94>0\)

  L'équation \(P(x)=0\) a donc deux solutions :

  • \(x_1=\dfrac{\frac12-\sqrt{\frac94}}{2\times\frac12}=\dfrac{\frac12-\frac32}{1}\color{red}=-1\)

  • \(x_2=\dfrac{\frac12+\sqrt{\frac94}}{2\times\frac12}=\dfrac{\frac12+\frac32}{1}\color{red}=2\)

• D'autre part, \(a=0,5>0\) la parabole est donc tournée vers le haut.

  \(P(x)<0\) entre ses racines \(x_1\) et \(x_2\) soit pour \(\color{red}x\in]-1 ;2[\)

• \(\begin{array}{|rcl}P(x)&=&0,5x^2-0,5x-1\\&=&0,5\left(x^2-x\right)-1\\&=&0,5\left(\left(x-0,5\right)^2-0,25\right)-1\\&=&0,5\left(x-0,5\right)^2-0,125-1\\&=&\color{red}0,5\left(x-0,5\right)^2-1,125\\&=&\color{red}\frac12\left(x-\frac12\right)^2-\frac{9}{8}\end{array}\)

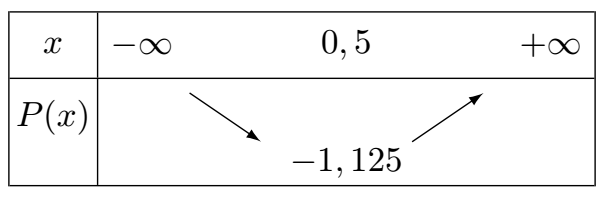
• Les coordonnées du sommet sont donc \(\color{red}(0,5 ;-1,125)\).

• \(a=0,5>0\), la parabole est donc tournée vers le haut.

Pour tout réel \(x\) :

\(\begin{array}{rcl}P(x+1)&=&0,5(x+1)^2-0,5(x+1)+c\\&=&0,5\left(x^2+2x+1\right)-0,5x-0,5+c\\&=&0,5x^2+x+0,5-0,5x-0,5+c\\&=&0,5x^2+0,5x+c\end{array}\)

\(P(x+1)-P(x)=0,5x^2+0,5x+c-\left(0,5x^2-0,5x+c\right)=0,5x+0,5x\color{red}=x\)

D'après la question précédente :

\(\begin{array}{ccccc}1&=&P(1+1)-P(1)&=&-P(1)+P(2)\\2&=&P(2+1)-P(2)&=&-P(2)+P(3)\\3&=&P(3+1)-P(3)&=&-P(3)+P(4)\\\cdots&=&\cdots&=&\cdots\\n&=&P(n+1)-P(n)&=&-P(n)+P(n+1)\end{array}\)

• En additionnant la colonne de gauche on obtient \(1+2+3+\cdots+n\)

• En additionnant la colonne de droite on obtient

  \(\begin{array}{rl}&-P(1)+\underbrace{P(2)-P(2)}_{=0}+\underbrace{P(3)-P(3)}_{=0}+\underbrace{P(4)-\cdots}_{=0}\cdots\underbrace{\cdots-P(n)}_{=0}+P(n+1)\\=&-P(1)+P(n+1)\end{array}\)

Donc pour tout entier naturel \(n\), \(\color{red}1+2+3+\cdots+n=P(n+1)-P(1)\)

D'après la question 3.a. \(P(n+1)=0,5n^2+0,5n+c\), donc :

\(\begin{array}{rcl}P(n+1)-P(1)&=&0,5n^2+0,5n+c-\left(\underbrace{0,5\times1^2-0,5\times1}_{=0}+c\right)\\&=&0,5n^2+0,5n+c-c\\&=&0,5n^2+0,5n\\&=&\frac12n^2+\frac12n\\&=&\frac12n(n+1)\\&=&\color{red}\frac{n(n+1)}{2}\end{array}\)

Finalement, \(\color{red}1+2+3+\cdots+n=\frac{n(n+1)}{2}\)