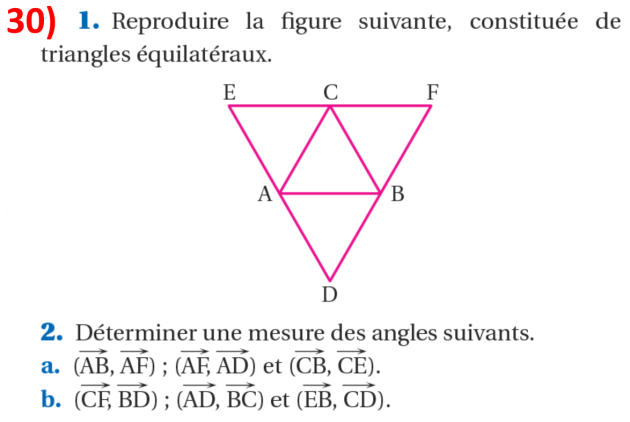
Ex 30

Question

Solution

Question 2, a)

Remarques :

  • Dans chaque triangle équilatéral, la bissectrice des angles est aussi la hauteur.

  • Les angles au sommet sont de 60° donc \(\dfrac \pi 3\).

  • \((\overrightarrow{AB};\overrightarrow{AF})\color{red}\underline{~=\dfrac{\pi}{6}}\) (figure[1])

  • \((\overrightarrow{AF};\overrightarrow{AD})=(\overrightarrow{AF};\overrightarrow{AB})+(\overrightarrow{AB};\overrightarrow{AD})=-\dfrac{\pi}{3}-\dfrac{\pi}{6}\color{red}\underline{~=-\dfrac{\pi}{2}}\) (figure[2])

  • \((\overrightarrow{CB};\overrightarrow{CE})=(\overrightarrow{CB};\overrightarrow{CA})+(\overrightarrow{CA};\overrightarrow{CE})=-\dfrac{\pi}{3}-\dfrac{\pi}{3}\color{red}\underline{~=-\dfrac{2\pi}{3}}\) (figure[3])

Solution

Question 2, b)

  • \((\overrightarrow{CF};\overrightarrow{BD})\color{red}\underline{~=-\dfrac{2\pi}{3}}\) (figure[4])

  • \((\overrightarrow{AD};\overrightarrow{BC})\color{red}\underline{~=\pi}\) (figure[5])

  • \((\overrightarrow{EB};\overrightarrow{CD})\color{red}\underline{~=-\dfrac{\pi}{3}}\) (figure[6])